حاسبة المثلث - أداة لحساب معلومات المثلثات بسهولة
استخدم حاسبة المثلث لحساب معلومات المثلثات بسهولة، بما في ذلك أطوال الأضلاع والزوايا والمساحة، مما يسهل عمليات الرسم الهندسي وحل المسائل الرياضية. هذه الحاسبة المثلثية المجانية تقوم بحساب الأضلاع، الزوايا، المساحة، الارتفاع، المحيط، الوسيط، بالإضافة إلى قيم أخرى ورسم تخطيطي للمثلث الناتج.
يرجى إدخال 3 قيم تتضمن جانباً واحداً على الأقل للحقول الستة التالية، ثم انقر على زر "احسب"
ماهو المثلث وأنواعه
المثلث هو مضلع له ثلاثة رؤوس. الرأس هو النقطة التي يلتقي فيها منحنيان أو خطوط أو حواف أو أكثر؛ في حالة المثلث، يتم ربط القمم الثلاثة بثلاثة خطوط تسمى الحواف. عادة ما يشار إلى المثلث برؤوسه. ومن ثم، يُشار إلى المثلث ذو الرؤوس a وb وc عادةً بالرمز Δabc. علاوة على ذلك، تميل المثلثات إلى وصفها بناءً على طول أضلاعها، بالإضافة إلى زواياها الداخلية. على سبيل المثال، المثلث الذي تكون فيه أضلاعه الثلاثة متساوية الطول يسمى مثلث متساوي الأضلاع، بينما المثلث الذي يكون فيه ضلعان متساويان في الطول يسمى متساوي الساقين. عندما لا يكون لأي من أضلاع المثلث أطوال متساوية، يشار إليه باسم مختلف الأضلاع، كما هو موضح أدناه.
علامات التجزئة الموجودة على حافة المثلث هي علامة شائعة تعكس طول الجانب، حيث يعني نفس عدد العلامات طولًا متساويًا. يوجد ترميز مماثل للزوايا الداخلية للمثلث، والتي يُشار إليها بأعداد مختلفة من الأقواس متحدة المركز الموجودة عند رؤوس المثلث. كما يتبين من المثلثات أعلاه، فإن طول المثلث وزواياه الداخلية مرتبطان ارتباطًا مباشرًا، لذا فمن المنطقي أن يكون للمثلث متساوي الأضلاع ثلاث زوايا داخلية متساوية وثلاثة أضلاع متساوية الطول. لاحظ أن المثلث الموجود في الآلة الحاسبة لا يظهر بمقياس الرسم؛ في حين أنه يبدو متساوي الأضلاع (ولديه علامات زاوية يمكن قراءتها عادةً على أنها متساوية)، إلا أنه ليس بالضرورة متساوي الأضلاع وهو مجرد تمثيل لمثلث. عند إدخال القيم الفعلية، ستعكس مخرجات الآلة الحاسبة الشكل الذي يجب أن يبدو عليه مثلث الإدخال. تنقسم المثلثات المصنفة بناءً على زواياها الداخلية إلى فئتين: قائمة أو مائلة. المثلث القائم هو مثلث تكون إحدى زواياه 90 درجة، ويشار إليه بقطعتين مستقيمتين تشكلان مربعًا في الرأس يشكل الزاوية القائمة. أطول حافة في المثلث القائم، وهي الحافة المقابلة للزاوية القائمة، تسمى الوتر. أي مثلث ليس مثلثًا قائمًا يتم تصنيفه على أنه مثلث مائل ويمكن أن يكون منفرجًا أو حادًا. في المثلث المنفرج، تكون إحدى زوايا المثلث أكبر من 90 درجة، بينما في المثلث الحاد تكون جميع الزوايا أقل من 90 درجة، كما هو موضح أدناه.
حقائق المثلث والنظريات والقوانين
- لا يمكن أن يكون للمثلث أكثر من رأس زاوية داخلية أكبر من أو تساوي 90 درجة، وإلا فلن يكون مثلثًا.
- مجموع الزوايا الداخلية للمثلث دائمًا ما يصل إلى 180 درجة بينما الزوايا الخارجية للمثلث تساوي مجموع الزاويتين الداخليتين غير المجاورتين له. هناك طريقة أخرى لحساب الزاوية الخارجية للمثلث وهي طرح زاوية الرأس محل الاهتمام من 180 درجة.
- مجموع طولي أي ضلعين في المثلث يكون دائمًا أكبر من طول الضلع الثالث.
- نظرية فيثاغورس: نظرية فيثاغورس هي نظرية خاصة بالمثلثات القائمة. في أي مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين الآخرين. ويترتب على ذلك أن أي مثلث تتوفر فيه أضلاعه هذا الشرط هو مثلث قائم الزاوية. هناك أيضًا حالات خاصة للمثلثات القائمة، مثل 30° 60° 90، 45° 45° 90°، و3 4 5 مثلثات قائمة تسهل العمليات الحسابية. حيث a و b ضلعان للمثلث، و c هو الوتر، يمكن كتابة نظرية فيثاغورس على النحو التالي:
a2 + b2 = c2
- قانون الجيب: النسبة بين طول ضلع المثلث وجيب الزاوية المقابلة له ثابتة. إن استخدام قانون الجيب يجعل من الممكن العثور على زوايا وجوانب مجهولة للمثلث بمعلومات كافية. عندما تكون الجوانب أ، ب، ج، والزوايا أ، ب، ج كما هو موضح في الآلة الحاسبة أعلاه، يمكن كتابة قانون الجيب كما هو موضح أدناه. وبالتالي، إذا كانت b وB وC معروفة، فمن الممكن العثور على c من خلال ربط b/sin(B) وc/sin(C). لاحظ أن هناك حالات عندما يستوفي المثلث شروطًا معينة، حيث يكون من الممكن وجود تكوينين مختلفين للمثلث في ضوء نفس مجموعة البيانات.
(a/sin(A))=(b/sin(B))=(c/sin(C))- بمعرفة أطوال الأضلاع الثلاثة لأي مثلث، يمكن حساب كل زاوية باستخدام المعادلة التالية. ارجع إلى المثلث أعلاه، بافتراض أن a وb وc هي قيم معروفة.
A = arccos((b2 + c2 - a2)/2bc)B = arccos((a2 + c2 - b2)/2ac)
C = arccos((a2 + b2 - c2)/2ab)
مساحة المثلث
- هناك عدة معادلات مختلفة لحساب مساحة المثلث، اعتمادًا على المعلومات المعروفة. من المحتمل أن المعادلة الأكثر شيوعًا لحساب مساحة المثلث تتضمن قاعدته b وارتفاعه h. تشير "القاعدة" إلى أي ضلع من أضلاع المثلث حيث يمثل الارتفاع بطول القطعة المستقيمة المرسومة من الرأس المقابل للقاعدة، إلى نقطة على القاعدة تكون متعامدة.
area = (1/2) × b × h
- بمعرفة طول الضلعين والزاوية بينهما، يمكن استخدام الصيغة التالية لتحديد مساحة المثلث. لاحظ أن المتغيرات المستخدمة تشير إلى المثلث الموضح في الآلة الحاسبة أعلاه.
area = (1/2) × ab × sin(C) = (1/2) × bc × sin(A) = (1/2) × ac × sin(B)- هناك طريقة أخرى لحساب مساحة المثلث تستخدم صيغة هيرون. على عكس المعادلات السابقة، لا تتطلب صيغة هيرون اختيارًا عشوائيًا لجانب كقاعدة أو قمة كنقطة أصل. لكن يشترط معرفة أطوال الأضلاع الثلاثة. مرة أخرى، في إشارة إلى المثلث الموجود في الآلة الحاسبة
area = √s(s - a)(s - b)(s - c)Where: s = (a + b + c)/2
الوسيط
يتم تعريف متوسط المثلث على أنه طول القطعة المستقيمة التي تمتد من قمة المثلث إلى منتصف الجانب المقابل. يمكن أن يحتوي المثلث على ثلاثة متوسطات، تتقاطع جميعها عند المركز الأوسط (موضع المتوسط الحسابي لجميع النقاط في المثلث) للمثلث. الرجوع إلى الشكل الوارد أدناه للتوضيح.
يتم تمثيل متوسطات المثلث بواسطة المقاطع الخطية ma وmb وmc. ويمكن حساب طول كل وسيط على النحو التالي:
حيث تمثل a وb وc طول ضلع المثلث كما هو موضح في الشكل أعلاه.
نصف القطر
نصف القطر هو نصف قطر أكبر دائرة يمكن وضعها داخل المضلع المحدد، وهو في هذه الحالة مثلث. نصف القطر متعامد على كل جانب من جوانب المضلع. في المثلث، يمكن تحديد نصف القطر من خلال إنشاء منصفين للزاوية لتحديد مركز المثلث. نصف القطر هو المسافة العمودية بين مركز المثلث وأحد أضلاعه. يمكن استخدام أي جانب من أضلاع المثلث طالما تم تحديد المسافة العمودية بين الضلع والمركز، حيث أن المركز، بحكم التعريف، متساوي البعد من كل جانب من جوانب المثلث
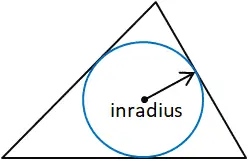
لأغراض هذه الآلة الحاسبة، يتم حساب نصف القطر باستخدام المساحة (المساحة) وشبه محيط المثلث بالإضافة إلى الصيغ التالية:
inradius = area/ss = (a + b +c)/2
حيث a، b، c هي أضلاع المثلث
دائرة نصف قطرها
يتم تعريف محيط القطر على أنه نصف قطر الدائرة التي تمر بجميع رؤوس المضلع، وهو في هذه الحالة مثلث. ومركز هذه الدائرة، حيث تلتقي جميع المنصفات المتعامدة من كل ضلع من أضلاع المثلث، هو محيط المثلث، وهو النقطة التي يقاس منها محيط نصف القطر. ليس من الضروري أن يكون محيط المثلث داخل المثلث. ومن الجدير بالذكر أن جميع المثلثات لها دائرة محيطية (الدائرة التي تمر عبر كل قمة)، وبالتالي محيط نصف القطر.
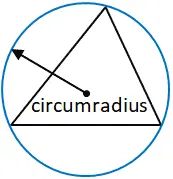
لأغراض هذه الآلة الحاسبة، يتم حساب نصف القطر باستخدام الصيغة التالية:
circumradius = a/2sin(A)حيث a أحد أضلاع المثلث، و A هي الزاوية المقابلة للضلع a
على الرغم من استخدام الضلع a والزاوية A، إلا أنه يمكن استخدام أي من الجوانب والزوايا المقابلة لها في الصيغة.